# 145 Binary Tree Postorder Traversal

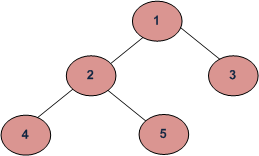
Definition: (a) Inorder (Left, Root, Right) : 4 2 5 1 3 (b) Preorder (Root, Left, Right) : 1 2 4 5 3 (c) Postorder (Left, Right, Root) : 4 5 2 3 1

這三種traversal的iterative解法都會長的類似這樣：

List<Integer> result = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();

TreeNode p = root;

while(!stack.isEmpty() || p!= null){
    if(p!=null){
        /*
        traverse 左邊或右邊的分支
        */
    }else{
        /*
        在某個分支已經走到底時，從stack pop出TreeNode
        再看要怎麼走
        */
    }
}

return result;

本題問的是postorder traversal，postorder之中root會在最後面。 解法是每遇到一個node就從result list的頭塞值進去，並且往右走，直到不能再往右了，就從stack中pop出來，取該node的左邊

Code

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        LinkedList<Integer> result = new LinkedList<>();

        TreeNode p = root;

        while(!stack.empty() || p != null){
            if(p!=null){
                stack.push(p);
                result.addFirst(p.val);
                p = p.right;
            }else{
                TreeNode node = stack.pop();
                p = node.left;
            }
        }

        return result;
    }
}

補上preorder和inorder的code

public List<Integer> preorderTraversal(TreeNode root){
        List<Integer> result = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();

        TreeNode p = root;

        while(!stack.isEmpty() || p!=null){
            if(p!=null){
                stack.push(p);
                result.add(p.val);
                p = p.left;
            }else{
                TreeNode node = stack.pop();
                p = node.right;
            }
        }

        return result;
    }

    public List<Integer> inorderTraversal(TreeNode root){
        List<Integer> result = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();

        TreeNode p = root;

        while(!stack.isEmpty() || p!=null){
            if(p!=null){
                stack.push(p);
                p = p.left;
            }else{
                TreeNode node = stack.pop();
                result.add(node.val);
                p = node.right;
            }
        }
    }

ref: https://leetcode.com/problems/binary-tree-postorder-traversal/discuss/45551/Preorder-Inorder-and-Postorder-Iteratively-Summarization